Thảo luận chạy song mã servo

[huyquynhbk]

ngoài lề một tý, cụ cần 1 cặp 400w thì báo em nhé. đang có 1 cặp 400w Samsung, nếu cụ thích combo song mã lắp luôn cho nó em cũng có luôn kaka

Vâng.thanks cụ.có gì các cụ giúp e nhá.

[CKD]

Báo cáo bác vấn đề là em nói ra thì nhiều người mất cơm. Và còn nhiều vấn đề nữa.
Em thách đố bác nào chạy được song mã. Chỉ cần 01 người trên diễn đàn này chạy được song mã thì em mất 01 triệu cho diễn đàn. Số tiền 01 triệu ấy được xung vào công quỹ của diễn đàn em tạm gọi là quỹ rượu.

PS: 01 triệu sẽ được chuyển vào tài khoản của diễn đàn trong vòng 24h nếu em thua cuộc.

Cái vụ 1 trẹo xem ra chỉ là chém gió hay nói phét thôi hả các bác. Vậy mà làm em cứ mừng hụt là quỹ ăn nhậu sẽ có cơ đấy.

[hanasimitai]

Cái vụ 1 trẹo xem ra chỉ là chém gió hay nói phét thôi hả các bác. Vậy mà làm em cứ mừng hụt là quỹ ăn nhậu sẽ có cơ đấy.

Lấy được tiền của em không dễ đâu bác. Bác đọc tài liệu em đưa lên có hiểu không mà đòi lấy tiền. Nếu em nhớ không nhầm thì bác còn chằng hiểu tốc độ cơ bản là gì mà?

[Nam CNC]

cái lưỡi không xương nhiều đường lắt léo , bác tốt nghiệp hệ nhà nước ra mà nên giỏi món này lắm , đấm vỡ mồm còn nói là gạt tay hơi quá còn được mà.


bác đổi nick thành "hentai lái gió" được rồi... mà hentai là gì tự tra tiếng nhật nhé.

[CKD]

Kaka!
Làm theo cái tài liệu... đúng là phét lác.
Bác bảo làm được... thì tôi đây bảo làm được, nếu cần thì tôi chứng minh qua hình ảnh. Bác bảo không được.. rồi đưa cái tài liệu của hãng. Hãng nó có bảo là nếu không làm như vậy thì không chạy được không?

Có thể có nhiều cái tui còn chưa rỏ, nên mới lang thang diễn đàn để tranh thủ học lóm thôi. Nhưng cái tôi nói là cái tôi làm. Chẵng như ai chăm chăm bóc phét mà éo làm được.

Chém gió cho vui mồm thì thằng nào chẵng chém được chứ. Tui đây nếu muốn cũng làm vô tư. Thử xem nhé.

Để gọi là chém gió thì tôi nói bác ngoài vụ phét lác mấy cái tài liệu ra thì biết éo gì về driver với servo mà song với mã. Vì ngoài cái trang tài liệu copy ra thì còn quái gì minh chứng đâu.
Còn tài liệu á... tui cũng có cả kho. Đọc hiểu hay không thì tự tui biết. Chỉ là nếu mọi thứ đều làm như hãng nói thì mấy ai diyer làm được. Mà làm theo hãng thì giỏi lắm cũng cở tầm thợ bảo trì thôi. Làm éo gì hơn được.

[phuocviet346]

Trình độ em thì kém quá không dám bàn luận, đọc từ đầu tới cuối tháy bác hentai đúng là "sửu nhi". Điều khiển đồng trục servo người ta làm phổ biến rồi bác ơi

[CKD]

Nói phét thật là ngứa miệng.. chắc tại mình không thuộc đạo ấy.

Còn nói thật thì như những gì đã nói. Chỉ là nối song song tín hiệu và chạy. Lưu ý là manual tuning hơi bị đuối. Đó là cách mà tôi đã làm và đã chạy trên máy.
Tất nhiên là không thể so sánh với hãng. Khi vận hành 2 servo sẽ có độ lệch nhất định. Nhưng với sự kết hợp kết cấu cơ khí tốt và tuning cẩn thận thì kết quả đủ mức đạt yêu cầu. Sản phẩm làm ra đủ để chấp nhận, bài toán chi phí & hiệu quả mang lại Ok.

Trở lại vấn đề.. là để tiếp cận với vụ chạy kết hợp 2 bộ servo, nói theo kiểu học thuật hay lý thuyết thì vô tư. Bên dưới sẽ QUOTE lại nội dung một bài viết trên web. Mà theo thôi được trình bày khá rỏ ràng lý do tại sao phải kết nối được 2 driver. Hay nói cách khác là cùng một driver mà điều khiển 2 motor độc lập. Chẵng qua là với dân DIYer thì khó lòng mà tiếp cận được những driver có được những tính năng ấy. Nên chẵng dám bàn nhiều. Mục đích cũng là muốn anh em nhanh chóng, tự tin làm và đạt được cái mình muốn. Tất nhiên.. cái ấy không thể tuyệt vời ông mặt trời được. Không tuyệt vời nhưng chấp nhận được & vẫn đáp ứng đủ nhu cầu.

Introduction

Figure 1. Box-in-box structure.
Synchronization motion control of multi-axis machine tools has become a significant issue due to the growing demand for high speed precise manufacturing. For such an application, two direct feed-drive linear servomotors are often adopted and arranged into a twin-parallel structure, the so-called “box-in-box” layout, to increase the thrust and stiffness of machine tools.The box-in-box structure adopts a pair of linear servomotors with mechanical coupling of one feed axis. Figure 1 shows an example in which the Y-axis is driven by the two linear motors coupled with the X-axis feed drive. An important requirement for high speed precision machining is the capability of the twin-parallel feed drives to follow the same command trajectories accurately for achieving a satisfactory positioning accuracy and also for reducing the synchronization error of the two parallel motors.

Strategies of the synchronous motion control technique can be classified into three categories: (1) synchronous master motion control, (2) master-slave motion control, and (3) relative dynamic stiffness motion control [1]. The framework of Category (1) is depicted in Figure 2, which is also called parallel synchronous control. As illustrated in Figure 2, the two servomotors receive the same motion command simultaneously and are controlled independently without considering the motion of the other. The advantage of this control scheme lies in its simple structure. However, accurate synchronous movement may not be guaranteed due to some possible effects such as unknown disturbances or unmatched model. This scheme is not suitable for the box-in-box machine tools since inherent disturbances always exist due to inevitable nonlinear dynamics, such as mechanical coupling. Note that asynchronous operation in motion control may result in diminished machining accuracy of the work-piece or even lead to breakage of the device.

To improve this shortcoming, Sarachik and Ragazzini proposed the master-slave control scheme of Category (2) and applied it to a biaxial system [2]. In comparison to the synchronous master motion control, the master-slave control operates in a cascade manner, enabling the slave servo system to follow the master with higher dynamic stiffness. Thus, the framework of master-slave control provides an alternative solution which allots a great deal of attention to synchronous motion control. As shown in Figure 3, a tandem control of two servo systems with velocity feedforward compensation was proposed by FANUC Ltd. to drive a single axis of motion [3]. Furthermore, another master-slave control based on speed/torque coupling was developed by SIEMENS [4].

The synchronous error can be eliminated in the master-slave framework if the disturbance occurs in the master. However, the servo lag between the master axis and the slave axis causes synchronization errors, while the unidirectional communication renders the master axis unable to detect the asynchronous movement when the slave axis encounters uncertain load disturbances. Therefore, the so-called relative dynamic stiffness motion control of Category (3) was proposed in which the synchronous error can be compensated by both axes. Figure 4 illustrates a position/velocity hybrid synchronous control proposed by Hsieh [5] with the concept of relative dynamic stiffness motion control. The same idea is also adopted by Yang [6] for controlling dual parallel linear servomotors. The key feature of relative dynamic stiffness motion control is that two motors compensate each axis in the velocity loop, but the position controller is only employed on the master. This framework can eliminate the servo lag error which occurs in the master-slave framework, while inharmonious movement in velocity loops can be compensated for in each axis. For further discussion of these three categories, one can refer to [1]. This paper utilizes relative dynamic stiffness motion control as the control strategy due to the benefits described above.


Figure 2. Parallel synchronous control.


Figure 3. Tandem control with velocity feedforward compensation [7].


Figure 4. Relative dynamic stiffness motion control of [5].
Much previous research has focused on the velocity synchronization problem of two-axis motion. Recently, great progress has been made in utilizing the cross-coupling concept to solve position synchronization of multiple motion axes. Chiu and Tomizuka provided a necessary coupling effect, which was introduced to each axis by the proper choice of a Lyapunov-like function [7]. In addition to actual position and velocity information, the resulting control law requires prior knowledge of the desired trajectories and their time derivatives. Sun proposed a new control framework for position synchronization of multiple motion axes by incorporating cross-coupling technology into the adaptive control architecture [8]. The above-mentioned approaches are commonly applied to multi-axis motion control systems rather than configurations, such as the "box-in-box" system.

In the "box-in-box" servo mechanism, an accurate model of the controlled plant is useful for the design of the synchronous control, particularly in the presence of mechanical coupling. Therefore, this paper presents an identification method to identify the effect of mechanical coupling. Figure 5 shows a gantry-type machine tool which is driven directly by three linear servomotors in which a pair of motors forms the X-axis coupling with the Y-axis. An identification method is employed to characterize the dynamics of the mechanical coupling and a synchronous control scheme is also developed for the X-axis to achieve synchronized motion control of the coupled systems. For clarification and simplicity, the error of motion between these two parallel servo systems in the Y-axis is hereafter defined as the "synchronization error", which is the target to be eliminated by the proposed controller. It is noted that non-zero synchronization error causes the coupling to bend and generates force acting on both driving motors.


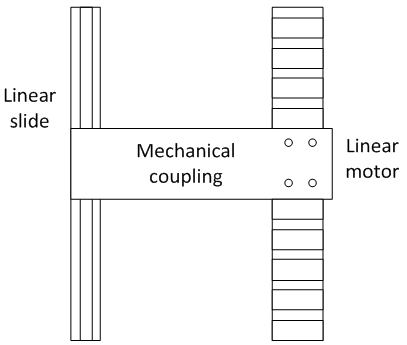
Figure 5. Gantry-type machine driven by a linear motor with a linear guide way.


Figure 6. System model from the thrust command to the output.


Figure 7. The linear motor driven machine tool.

QUOTE từ nguồn http://www.ausmt.org/index.php/AUSMT/article/view/72/25
Các bán nên vào trang & đọc kỹ, phía bên dưới còn nhiều phân tích & tính toán bổ ích.

[CKD]

Một số tài liệu bảo hộ cho các vấn đề này
https://www.google.ch/patents/US20100181955
http://www.google.co.ug/patents/EP0717331A1?cl=zh

[thuhanoi]

Kaka!
..................... Mà làm theo hãng thì giỏi lắm cũng cở tầm thợ bảo trì thôi. Làm éo gì hơn được.

. Right

[hanasimitai]

cái lưỡi không xương nhiều đường lắt léo , bác tốt nghiệp hệ nhà nước ra mà nên giỏi món này lắm , đấm vỡ mồm còn nói là gạt tay hơi quá còn được mà.


bác đổi nick thành "hentai lái gió" được rồi... mà hentai là gì tự tra tiếng nhật nhé.

Không biết là cái ông Pín này lắp vít me chạy được bao lâu mà to mồm thế nhỉ.

[Nam CNC]

bác hentai đi chổ khác chơi , không có chuyện gì cho bác lên tiếng ở đây cả , cứ làm ma xó ngồi góc xó mà đọc đi ...

Em làm được gì như thế nào anh em khác đều biết ứ cần bác quan tâm.

[terminaterx300]

bác hentai đi chổ khác chơi , không có chuyện gì cho bác lên tiếng ở đây cả , cứ làm ma xó ngồi góc xó mà đọc đi ...

Em làm được gì như thế nào anh em khác đều biết ứ cần bác quan tâm.

Về nghịch pín thằng ku ở nhà đi, để anh ấy thể hiện đủ oài

anh ấy éo có cái clip nào show hàng mà chém gió là chính thoai.

ở đây nhiều thằng nó đi xa lắm luôn rồi cơ mà cứ tưởng như đáy giếng

[hanasimitai]

Về nghịch pín thằng ku ở nhà đi, để anh ấy thể hiện đủ oài

anh ấy éo có cái clip nào show hàng mà chém gió là chính thoai.

ở đây nhiều thằng nó đi xa lắm luôn rồi cơ mà cứ tưởng như đáy giếng

Bác lại tự sướng rồi, ở đây là cái vựa ve chai.

[nhatson]

Bác lại tự sướng rồi, ở đây là cái vựa ve chai.

hihi thế mà có dân high class nào đó cứ lượn lờ coi ve chai
thế thì ve chai cũng là cái thú tao nhã

[terminaterx300]

Bác lại tự sướng rồi, ở đây là cái vựa ve chai.

đúng là ếch, mày đã mua dc hàng brandnew chính hãng nào chưa mà hù ai thế hả hentai

ở đây có nhiều đại gia mua hàng chính hãng rồi ếch ơi

[thuhanoi]

Đang nói xẹc vô thôi đưa đống ve chai ni lên chào bác hen tai




Nhớ tra date nhá

[saudau]

đúng là ếch, mày đã mua dc hàng brandnew chính hãng nào chưa mà hù ai thế hả hentai

ở đây có nhiều đại gia mua hàng chính hãng rồi ếch ơi

Nếu mình nhớ ko lầm thì con ếch cái miệng nó rộng mà 2 con mắt nó lòi ra ngoài phải ko bác?

[secondhand]

Nếu mình nhớ ko lầm thì con ếch cái miệng nó rộng mà 2 con mắt nó lòi ra ngoài phải ko bác?

Miệng nó rộng nên la to, con mắt lòi ra chỉ 1 nhiệm vụ duy nhất ... là đề phòng mấy tên soi ếch. Nếu mắt nó mà ti hí thì cả ông và tui không biết thịt ếch nướng nó ngon như thế nào


@ hentai
"Chẳng thà mình không nói, để người ta tưởng mình ngu, còn hơn mở miệng ra, để người ta không còn nghi ngờ gì nữa"

-Mark Twain

Up cái đi ngủ khakha

[hanasimitai]

Miệng nó rộng nên la to, con mắt lòi ra chỉ 1 nhiệm vụ duy nhất ... là đề phòng mấy tên soi ếch. Nếu mắt nó mà ti hí thì cả ông và tui không biết thịt ếch nướng nó ngon như thế nào


@ hentai
"Chẳng thà mình không nói, để người ta tưởng mình ngu, còn hơn mở miệng ra, để người ta không còn nghi ngờ gì nữa"

-Mark Twain

Up cái đi ngủ khakha

Dạy người khác làm éo gì. về nhà lo mà day vợ con đi.

[hanasimitai]

đúng là ếch, mày đã mua dc hàng brandnew chính hãng nào chưa mà hù ai thế hả hentai

ở đây có nhiều đại gia mua hàng chính hãng rồi ếch ơi

Bố mày éo chơi hàng chế với hàng tàu hiểu chưa con.